学生諸君！
家にいても暇でしょう。
ということで、数学大好き あおもり むなかた から、数学の問題を出します。
「アオモリ探検隊」なのにそれでいいのか！？という野暮なつっこみは無しで。
自粛ムードの中、なかなか普通の投稿がしずらくて・・・。でも何か投稿したいし。

さて『ケーキの切れない非行少年たち』という本をご存知でしょうか。
昨年ベストセラーになったこちらの書籍。
「非行少年は何故ケーキを3等分できないのか」ってのがこの本のテーマになっています。（ちなみに読んでません。ごめんなさい）

普通はベンツのエンブレムのように3等分するのをパッと思いつくんじゃないでしょうか。
でもちょっと待って！これって包丁3回入れないといけないじゃん！
3等分なら2回でいけるっしょ！と思った時、さてどこに包丁を入れれば良いでしょうか。

というのを延々一週間も考えてみました。まぁ寝る前の30分×7って感じなのですが。
数学は睡眠導入剤ですね。いつの間にか眠れます。

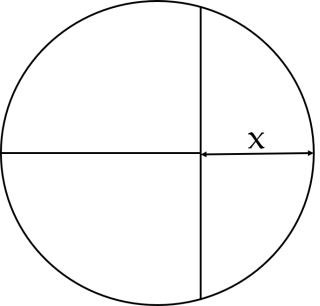
こんな図を考えてみます。
右端、3分の1が切り出せれば、残りは真ん中からばっさり2等分できますね。
ということで、包丁の挿入位置、ｘの値を求めてみましょう。
ちなみにケーキの半径はＲとします。
ヒントは右端の半月型の円の面積を求めること。
答えはずーーっと下にスクロール！

回答

右端の半月の面積を S、x’ = R – x とすると
S = R^2*acos(x’/r) – x’*√(R^2 – x’^2)

これが円の3分の1になれば良いので、以下の方程式が成り立つ。

π*R^2/3 = R^2*acos(x’/R) – x’*√(R^2 – x’^2)

acos の中に x’ があったり、素の x’ があったり、数学的な解が望めないので、数値計算にて近似値を算出。
R = 1 の時で、x’ ≒ 0.265
つまり x = 0.735

R にいろいろな値を取り、シミュレーションすると、x = R*0.735 なことが分かる。
つまり、直径を2として、割合として右端から 0.735 の位置に包丁を入れると3分の1が切り出せる。

ちなみに 0.735 だと目視が難しいので、0.75 としてしまえば 4分の3 で分かりやすい。
まとめると、ホールケーキの直径を8等分して右から 3 の位置に切れ込みを入れれば3等分できる。

いきなり S = の式が出てきたり（扇形の面積から三角形の面積を引いてます）、数値計算で無理矢理解を出すとか、いろいろ力技な部分がありますがご了承ください。
何にしても切った後にいびつな形になるので 一生使うことはないと思いますが、ホールケーキを切るときの小ネタとして「ケーキ3等分するのってすげー難しいんだぜ」と子供に話して聞かせれば非行少年にならず、数学大好き少年になると思います！